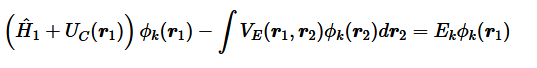非制限ハートリー＝フォック法

非制限ハートリー＝フォック法(ひせいげんハートリーフォックほう、英: Unrestricted Hartree–Fock method、UHF法)とは、${\displaystyle \alpha }$スピンと${\displaystyle \beta }$スピンの電子数が一致しないような、開殻分子を扱うための、最も一般的な分子軌道法である。スピン軌道ごとに異なる空間軌道を用いるという特徴がある 。

特徴

後述のスピン汚染の問題にもかかわらず、制限開殻ハートリー-フォック(ROHF)法と比較すると、非制限ハートリー–フォック法(UHF)法は頻繁に用いられる。

ROHF法と比較して、UHF法の方がコード実装が単純で、より容易にpost-HF法へ発展させられるためである。また、ROHF法では異なるフォック演算子が同一の波動関数を与えることがあるが、UHF法ではユニークな波動関数を与える。

非制限ハートリー-フォック法はGaston Berthierにより発見され、その後ジョン・ポープルにより発展した。ほとんどの第一原理計算プログラムで利用できる。

ポープル–ネスベット方程式

制限ハートリー-フォック法では、スレーター行列式の中で空間軌道と各スピン関数を乗じることで同一の空間軌道を2度用いている。 一方、非制限ハートリー-フォック法では${\displaystyle \alpha }$軌道と${\displaystyle \beta }$軌道に対して、異なる空間軌道を用いる。 このような考え方はDifferent Orbitals for Different Spins(DODS)と呼ばれている。 DODSを適用すると連立したローターン–ホール方程式の組が得られる。 これの式の組は、ポープル–ネスベット方程式（英: Pople-Nesbet equation)と呼ばれる 。

${\displaystyle {\begin{aligned}{\boldsymbol {F}}^{\alpha }{\boldsymbol {C}}^{\alpha }&={\boldsymbol {S}}{\boldsymbol {C}}^{\alpha }{\boldsymbol {\epsilon }}^{\alpha }\\{\boldsymbol {F}}^{\beta }{\boldsymbol {C}}^{\beta }&={\boldsymbol {S}}{\boldsymbol {C}}^{\beta }{\boldsymbol {\epsilon }}^{\beta }\end{aligned}}}$

ここで、${\displaystyle {\boldsymbol {F}}^{\alpha }}$と${\displaystyle {\boldsymbol {F}}^{\beta }}$はそれぞれ${\displaystyle \alpha }$軌道と${\displaystyle \beta }$軌道のフォック行列である。同様に、${\displaystyle {\boldsymbol {C}}^{\alpha }}$と${\displaystyle {\boldsymbol {C}}^{\beta }}$はそれぞれ${\displaystyle \alpha }$軌道と${\displaystyle \beta }$軌道の展開係数を示す。${\displaystyle {\boldsymbol {S}}}$は与えられた基底関数に対応する重なり行列を表す。 ${\displaystyle {\boldsymbol {\epsilon }}^{\alpha }}$と${\displaystyle {\boldsymbol {\epsilon }}^{\beta }}$ は${\displaystyle \alpha }$軌道と${\displaystyle \beta }$軌道の軌道エネルギーからなる対角行列を表す。

軌道係数は全電子が構成する平均場のもとで最適化されるため、各々のフォック行列は${\displaystyle \alpha }$軌道と${\displaystyle \beta }$軌道両方に依存する。したがって、上式を連立させて、自己無撞着に解く必要がある。 最終的には${\displaystyle \alpha }$軌道の軌道係数と軌道エネルギー、および${\displaystyle \beta }$軌道の軌道係数と軌道エネルギーが同時に得られる。

スピン汚染

各スピン軌道に異なる空間軌道を用いることで構成した単一のスレーター行列式は、 全スピン演算子${\displaystyle {\boldsymbol {S}}^{2}}$に対応した、満足のいく固有関数にはならないという欠点がある。 基底状態には励起状態が混入しており、これをスピン汚染と呼ぶ。

${\displaystyle \alpha }$軌道の電子数が${\displaystyle \beta }$の電子数よりも1つだけ多いとき、その基底状態は二重項状態となる。 ${\displaystyle {\boldsymbol {S}}^{2}}$の期待値、${\displaystyle \langle {\boldsymbol {S}}^{2}\rangle }$は${\displaystyle {\tfrac {1}{2}}({\tfrac {1}{2}} 1)=0.75}$ になる必要があるが、得られる電子状態には四重項状態が混入しているため、実際は${\displaystyle 0.75}$よりも大きい値を示す。 同様に三重項状態では${\displaystyle \langle {\boldsymbol {S}}^{2}\rangle =1(1 1)=2}$となるべきだが、五重項状態の混入によりこれよりも大きい値が得られる。 非制限ハートリー-フォック計算を行う際は、常にこのようなスピン汚染に配慮しなければならない。 例えば、二重項の計算で${\displaystyle \langle {\boldsymbol {S}}^{2}\rangle }$が0.8以下ならば問題はないと思われる。 しかし、もし1.0以上の値を取るようならば、良い結果とは言えず、非制限ハートリー-フォック計算とは別のアプローチが必要になるだろう。 スピン汚染についてこのように判断を下すには経験が必要である。

一重項状態の系においても、スピン汚染の悪影響を受けることがある。 例として水素分子の解離が挙げられる。 スピン汚染された状態の点、 コールソン＝フィッシャー点 (英: Coulson–Fischer point) ではエネルギー曲線が不連続になる 。

出典

関連項目

• ハートリー-フォック法
  • 制限開殻ハートリー-フォック法
• 分子軌道法
• 非経験的分子軌道法