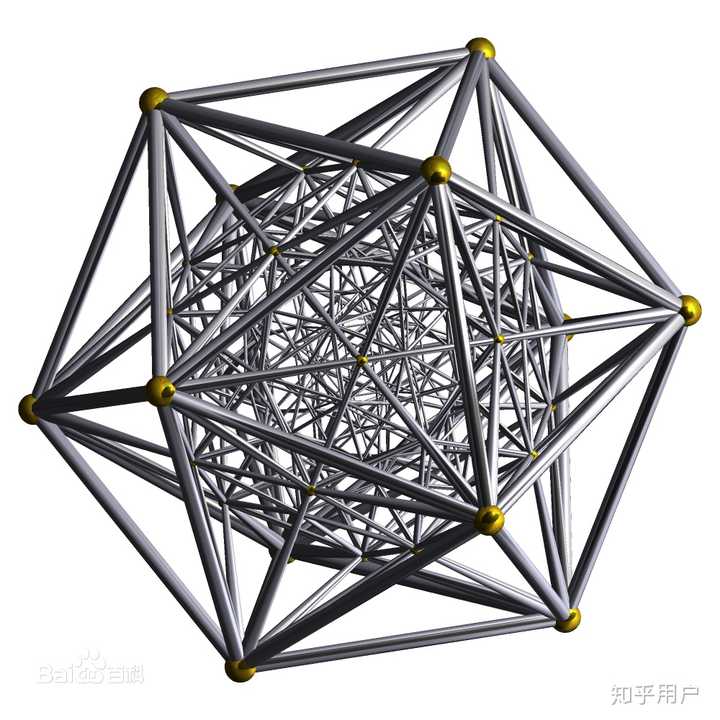
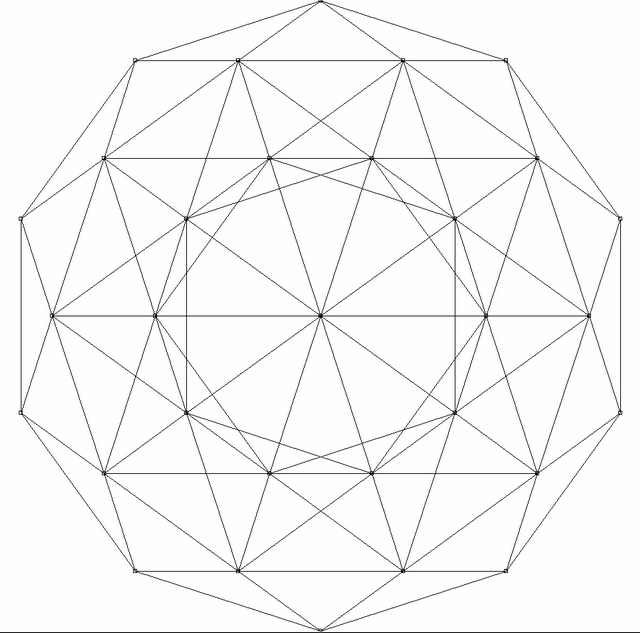
正六百胞体(せいろっぴゃくほうたい,Regular hexacosichoron)とは、 四次元正多胞体の一種で600個の正四面体からできており、三次元の正二十面体に相当する。標準正多胞体ではない。
- 胞(構成立体):正四面体600個
- 面:1200枚の各正三角形に正四面体2個が集まる。
- 辺:720本の各辺に正三角形5枚、正四面体5個が集まる。これは正二十面体の各頂点に辺5本、正三角形5枚が集まることに相当する。
- 頂点:120個の各頂点に辺12本、正三角形30枚、正四面体20個が集まる。これは正二十面体が12個の頂点、30本の辺、20枚の正三角形を持つことに相当する。
- 双対:正百二十胞体
- シュレーフリの記号:{3,3,5}
頂点座標
120個の頂点の座標は次の通り。ここで φ は黄金比 (1 √5)/2 である。
- (±1, ±1, ±1, ±1) (複号任意)の全ての置換 16個
- (±2, 0, 0, 0) (複号任意)の全ての置換 8個
- (±φ, ±1, ±φ-1, 0) (複号任意)の全ての偶置換 96個
脚注